课程说明

 

    •  
      高级中学数学，MathCounts / AMC 8-10问题

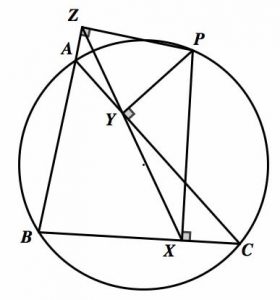
      本课程涵盖了中学数学的主要内容。学生将掌握这些课程，同时解决MathCounts，AMC-8，AMC 10和类似比赛的挑战性问题。在这个促进大脑开发的课程中，学生超越了共同核心标准。学生还将解决数学难题和密码，并学习传统学校环境通常无法涵盖的课程。

      推荐年级 虽然我们不按年级限制学生，但本课程通常建议4至8年级的学生。

      课程描述 本课程将使学生熟悉预代数、代数I、几何、数论和组合学中的基本概念和技巧。我们将特别强调解决问题，学生将不断受到创造性思考的挑战。

      比赛准备: MathCounts, AMC 8, AMC 10.

      课程目标: 完成本课程后，学生将：

      1.完全掌握标准的预代数、代数I和几何课程中涵盖的概念，以及传统学校课程中未涉及的课程。
      2.能够解释和使用组合、数论和几何中使用的重要定理和技术。
      3.能够将不熟悉的问题减少到基本原则，并巧妙地运用他们学到的技术寻找解决方法中的捷径。

      教学理念： 我们相信，建立良好的解决问题的能力与了解大量定理一样重要（或更重要）。因此，虽然课程将涵盖相当数量的材料，但主要重点是建立解决问题的直觉，并培养学生在面对从未见过的一系列问题时进行创造性思考。

      课堂参与： 学生应积极参加课堂。 我们将采用苏格拉底方法，这是学生和教师之间的合作机会，以激发批判性思维。学生还将与同学合作，同时解决具有挑战性的问题。

      课程： 课程由CyberMath 学院拥有和版权。 课程材料由来自全球各地着名比赛的独特混合问题组成，还有许多历史问题和迷人的谜题。

      有关夏令营出勤选择的信息（学年课程涵盖所有课程）

      代数

      比率和比例
      •代数表达式
      • 线性方程组
      • 功能
      •不平等
      •多项式表达式
      •帕斯卡的三角形
      •二项式定理
      •二次方程

      组合学

      •计数
      •统计
      •概率
      •排列
      • 组合

      数论

      •整除性
      •最大公因數
      •素数因子分解
      •有理和指数
      •模块化算术
      •序列和系列
      •高斯公式

      几何

      • 角度
      • 三角形
      • 勾股定理
      •多边形
      •圈子
      •周长，面积和体积
      •坐标几何
      •3D几何

 

    •  
      具有AMC 10/12问题的高级数学

      本课程为学生参加美国数学竞赛10和12以及AIME的非证明部分做好准备。 所教授的课程包括整个高中课程，包括三角学，高等代数，预先计算和高级几何，但排除微积分。 我们的课程还包括传统学校课程之外的一些额外的挑战性和激发大脑的课程。

      推荐年级： 虽然我们不按年级限制学生，但本课程通常建议7至8年级的学生。

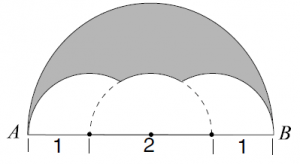      课程描述： 本课程将使学生熟悉代数II、前微积分、组合、数论和几何中的基本概念和技巧。我们将特别强调解决问题，学生将不断受到创造性思考的挑战。

      比赛准备： AMC 10/12, AIME, ARML, Mandelbrot, Purple Comet.

      课程目标： 完成本课程后，学生将：

      完全掌握标准代数II和预微积分课程中涵盖的概念，以及更高级的课程（如Vieta公式、复数和系列操作）。

      能够解释和使用组合、数论和几何中使用的重要定理和技术。

      能够将不熟悉的问题简化为基本原则，并巧妙地运用他们学到的技术来找到解决方法中的捷径。

      教学理念： 我们相信，建立良好的解决问题的能力与了解大量定理一样重要（如果不是更重要）。因此，虽然课程将涵盖相当数量的材料，但主要重点是建立解决问题的直觉，并培养学生在面对他们从未见过的一系列问题时进行创造性思考。

      课堂参与： 我们将采用苏格拉底方法，这是学生和教师之间的合作机会，以激发批判性思维。 学生还将与同学合作，同时解决具有挑战性的问题。

      课程： 课程由CyberMath 学院拥有和版权。 课程材料由来自全球各地着名比赛的独特混合问题组成，还有许多历史问题和迷人的谜题。

       

      本课程涵盖的课程

      代数

      – 二次方程式/判别式和圆锥曲线
      – 方程组
      -多项式除法
      – 理性根定理
      – 代数的基本定理
      -韦达定理
      – 序列和系列
      – 归纳
      – 激进分子和合理化分母
      – 代数因子分解
      – 复数
      – 不平等
      – 公式
      – 指数和对数

      组合学

      – 基本计数：可构造和余函数
      – 集合，双射和逻辑
      – 排容原理
      – 组合和排列
      – 帕斯卡三角形
      – 二项式定理
      – 组合等式
      – 鸽子原则
      – 期望值
      – 隔板法
      – 递归
      – 斐波纳契数

      数论

      – 质因子分解
      – 可分性规则
      – 欧氏算法
      – 丢番图方程
      – 贝祖等式
      – 模块化算术和指数
      – 费马小定理
      – 威尔逊定理
      – 中国剩余定理
      – 乘法函数
      – 欧拉定理

      几何

      – 全等及相似三角形
      – 三角形的特殊部分
      – 三角区公式
      – 四边形
      – 多边形中的角度
      – 圆周角的圆
      – 一点力量
      – 立体几何
      – 三角为直角三角形
      – 单位圆与弧度
      – 三角恒等式
      – 正弦与余弦定理
      – 极坐标和复数的几何

      点击下方查看示例讲义

 

如果您想获得有关AMC 8,10,12和AIME比赛的更多信息，请访问美国数学协会的美国数学竞赛 （AMC）页面。

2-想要超越学校级数学的学生

可供选择的课程：

– AIME问题的数学证明

本课程是我们数学奥林匹克计划的一部分。您可以在下面找到有关我们数学奥林匹克计划的更多信息。

 

 

    •  
      数学奥林匹克项目水平

      若要了解哪种课程最适合您，请查看以下信息：

      本课程有两个部分：

      AIME问题的数学证明 具有AIME问题的数学证明对于能够轻松获得AIME资格并解决考试前半部分问题的学生。这些学生可能的目标是获得USA(J)MO的资格，并在奥林匹克运动会中有一个愉快的开始。

      USA(J)MO: 对于已经可以轻松获得USA(J)MO资格的学生，并且他们的目标是获得高分。

       

      第一：请在下面确定您的等级

      （1）从AMC开始，试图获得AIME资格

      （2）可以解决AIME上的2个问题，希望能解决8个问题

      （3）可以解决AIME上的6个以上问题，希望能解决13个问题

      （4）有资格获得USA(J)MO，希望解决一两个问题

      （5）可以解决一两个USA(J)MO问题并解决困难的USAJMO或中型USAMO问题

      （6）旨在解决USAMO的最终P3 / P6问题

      第二：了解我们数学奥林匹克计划中的曲目

      我们的数学奥林匹克计划有两个部分：

      入门级数学奥林匹克课程与计算（高级AIME与证明）

      * 先决条件：AIME 6+

      * 旨在获得高AIME分数，以及USA(J)MO的几个问题

      高级数学奥林匹克课程（USAJMO

      * 先决条件：始终符合USA(J)MO资格

      * 旨在在USAMO获得14+

      第三：安置

      – 如果你在1级或2级，你应该报名参加我们的高级数学与AMC 10/12问题课程。其涵盖了AMC 10/12和AIME的非证明问题。

      – 如果你在3级或4级，你应该注册我们的高级AIME和证明课程。

      – 如果你在5级或6级，你应该报名参加我们的USA(J)MO课程。

 

    •  
      数学奥林匹克课程

      这个程序有两个部分：

      高级AIME与证明： 适合那些能够轻松获得AIME资格并解决考试前半部分问题的学生。

      USA(J)MO: 这些学生可能的目标是获得USA(J)MO,资格，并在奥林匹克运动会上有一个愉快的开始。

      这两个部分在任何一年都有重叠。 课程以三年为一周期。

      比赛准备： AIME, HMMT, USA(J)MO, IMO.

      课程： 该课程为期三年，因此学生可以在两个轨道上重复课程总计三次。夏季和全年的材料不相交。

      下方列出了所涵盖课题的详细列表。并非所有年份都出现所有课程。 大多数课程出现多年，但每次出现在三年周期中都会有不同的例子和问题。

      课程的每次迭代都包含几个练习考试。

      1- 课程仅出现在具有证明的高级AIME中

      代数

      • 对称多项式。 维塔公式、牛顿和，基本对称多项式的基本定理。
      • 对数。计算问题和涉及对数的方程。
      • 三角函数公式。 涉及三角函数代数问题。
      • 介绍公式。 奥林匹克式公式方程介绍。 替代、注入与满射，柯西函数方程。
      • 不等式。 介绍奥林匹克式的不平等。 AM-GM和Cauchy-Schwarz。

      组合学

      • 概率计算。 随机变量、期望值、期望线性。
      • 枚举。 计算计数问题。
      • 单变量和不变量。 Finite processes.

      几何

      • 计算几何。 欧几里德几何中的AIME式问题。角度追逐。
      • 三角函数。
      • 初等几何。 角度追逐、点的力量、位似变换。
      • 复数基础知识。几何中复数的介绍。

      数论

      • 使用模运算进行计算。 费马，威尔逊，中国剩余定理。
      • 丢番图方程。 奥林匹克式丢番图方程介绍。
      • 中国剩余定理。

      2- 出现在两个部分中的课程

      代数

      • 生成函数。 它们在组合总和中的用途。
      • 线性递归和有限差分。
      • 和。 交换汇总顺序。
      • 多项式。 代数、因子分解，根基本定理。

      组合学

      • 重量和着色。
      • 归纳和递归。
      • 期望和双重计算的线性。
      • 算法。 涉及离散时间过程的组合问题。
      • 图论。 定义和问题。
      • Ad-Hoc构造。
      • 矩形网格问题。

      几何

        • 点的力量。
        • 位似
        • 共同的结论。

      数论

          • 可分性和欧几里得算法。 限制剩余部分。
          • 查看指数。 p-adic评估，解除指数。
          • 命令。形式为a2 + b2 的素数。 原始根源。

      3- 仅出现在USA(J)MO的课程

      代数

          • 功能方程。 USAMO / IMO级别的功能方程更加困难。
          • 高级不等式。 詹森和舒尔。 捏造，平滑。
          • 分析和微积分。 理解微积分中的完整定理陈述以及它们如何应用于奥林匹克问题。分化与根的多样性的关系。 拉格朗日乘数。 紧凑。

      组合学

          • 高级图论。 涉及图表的奥运会问题更加困难
          • 高级算法。
          • 游戏和流程。

      几何

          • 投影几何。 谐波束，极点和极性。
          • 反转。
          • 螺旋相似性。
          • 复数。 应用于问题。
          • 重心坐标。 应用于问题。

      数论

          • 数论中的结构。
          • 整数多项式。 不可约性，最小多项式，伽罗瓦理论的味道。
          • 二次互易。 勒让德符号。